. DEFINISI
Turunan fungsi ( diferensial ) adalah fungsi lain dari suatu fungsi sebelumnya, misal fungsi f menjadi f’ yang mempunyai nilai tidak beratuhan atauTurunan merupakan tingkat perubahan sesaat sebuah fungsi terhadap salah satu variabelnya. Tingkat perubahan fungsi f(x) untuk setiap nilai x, yaitu turunan f(x), dapat dinyatakan dengan rumus:
Turunan Fungsi Aljabar
Berikut ini rumus turunan untuk bentuk fungsi aljabar. Rumus ini didapat dari penjabaran rumus turunan di atas.
- Jika y = k, maka y’ = 0
- Jika y = x, maka y’ = 1
- Jika
![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%3Dx%5En&bg=ffffff&fg=000&s=0) , maka
, maka ![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%27+%3Dn+%5Ccdot+x%5E%7Bn-1%7D&bg=ffffff&fg=000&s=0)
- Jika
![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%3Dax%5En&bg=ffffff&fg=000&s=0) , maka
, maka ![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%27+%3Dan+%5Ccdot+x%5E%7Bn-1%7D&bg=ffffff&fg=000&s=0)
KAIDAH - KAIDAH DIFERENSIAL
1. Diferensiasi Konstanta
Jika y=k , dimana k adalah konstanta , maka dy/dx = 0
Contoh : y = 10 , maka = 0
Atau lebih mudahnya kalau kita mengganti simbol dy/dx menjadi y’ , misalnya :
y = 100 → y’ = 0
y =1/2 → y’ = 0
2. Diferensiasi Fungsi Pangkat
jika y = xn dan adalah konstanta maka dy/dx = n.Xn-1
Contoh :
1. y = x7
y’ = 7x6
2. y = x-8
y’= -8x-9
3. Diferensiasi Perkalian Konstanta dengan fungsi
Jika y=kv dan v=h(x) maka dy/dx = k dv/dx
Contoh :
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
y= 5x-8 → y’= -40x-9
y= 6x5 → y’ = 30x4
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
4. Diferensiasi Pembagian Konstanta Dengan Fungsi
Jika y= k/v , dimana v=h(x) , maka dy/dx = k dv/dx / v2
Contoh :
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
y’=32x7
5. Diferensiasi Penjumlahan / pengurangan fungsi
Jika y = u ± v, dimana u = g(x) dan v = h(x) , maka dy/dx = du/dx ± dv/dx
Contoh :
y = 4x2 + x3 misalkan u = 4x2 → du/dx = 8x
v = x3 → du/dx = 3x2 , maka dy/dx = 8x + 3x2
y = -2x-1+ 4x + 8 , maka y’= 2x-2+ 4
6. Diferensiasi Perkalian Fungsi
Jika y=uv, dimana u = g(x) dan v=h(x)
Maka dy/dx= u dv/dx + v du/dx
Contoh :
- y = (4x2) (x3)
Misalkan u = 4x2 → du/dx = 8x
v = x3 → dv/dx = 3x2
Maka dy/dx = u dv/dx + v du/dx
= (4x2) (3x2) + (x3) (8x)
= 12x4+ 8x4
= 20x4
2. y = (8x2) (x4)
Misalkan u = 8x2 → du/dx = 16x
v = x4 → dv/dx = 4x3
Maka dy/dx = u dv/dx + v du/dx
= (8x2) (4x3) + (x4) (16x)
= 32x5+ 16x5
= 48x5
7. Diferensiasi Pembagian Fungsi
Jika y = U/V , dimana U = g(x) dan V=h(x)
Maka y’= VU’-UV’ / V2
Contoh :
- y = U/V → y = (4x2) / x3
y’= x3(8x) – (4x2). 3x2 / (x3)2
= 8x4-12x4 / x6
= -4x4/ x6
= -4x-2
2. y = (12x2) / x5
y’= x5(24x) – (12x2) . 5x4 / (x5)2
= 24x6 – 60x6 / x10
= -36 x6 / x10
= -36 x-4
. PERUBAHAN
1. Laju Perubahan Nilai Fungsi
Laju perubahan suatu fungsi dibedakan menjadi dua ,yaitu laju perubahan rata-rata dan laju perubahan sesaat.
a. Laju Perubahan Rata-Rata
Jika diketahui suatu fungsi y = f(x) maka laju perubahan rata-rata fungsi y = f(x) pada interval dirumuskan dengan .
Contoh :
Diketahui suatu fungsi f(x) = 2x² + 5x + 3 dengan daerah asal = {x|x .
Jika -2 tentukan laju perubahan rata-rata fungsi f(x) terhadap x.
Penyelesaian:
f(x) = 2x² + 5x + 3
untuk x = -2 maka f(-2) = 2(-2)² + 5(-2) + 3 = 1
untuk x = 3 maka f(3) = 2(3)² + 5(3) + 3 = 36
Jadi, laju perubahan rata-rata fungsi f(x) adalah 7.
Laju Perubahan Sesaat
Laju perubahan sesaat suatu fungsi y = f(x) adalah laju perubahan yang sesaat, artinya perubahan pada interval
Contoh:
Diketahui suatu persegi panjang dengan panjang 5x cm dan lebar 2x cm. tentukan perubahan luas persegi panjang terhadap panjang sisi x ketika x = 4 cm
Penyelesaian:
Luas persegi panjang = L = p . l = 5x . 2x = 10x²
Luas perubahan sesaat L = f(x) adalah:
=80+0
=80
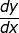 dari setiap fungsi Implisit dibawah ini!
dari setiap fungsi Implisit dibawah ini!
