Definisi Turunan Fungsi Implisit yaitu fungsi yang memuat dua variabel atau lebih, variabel-variabel tersebut terdiri dari variabel bebas dan variabel tidak bebas, biasanya variabel-variabel tersebut dinyatakan dalam x dan y dimana variabel x dan y terletak didalam satu ruas sehingga tidak dapat dipisahkan menjadi ruas yang berbeda (baca : ruas kiri dan ruas kanan) seperti halnya fungsi eksplisit.
|
Turunan Fungsi Implisit Serta bentuk umum nya
Secara umum bentuk turunan fungsi implisit adalah f(x,y) = 0, mencari turunan fungsi implisit sama dengan mencari solusi bentuk umumnya dan prinsipnya tidak jauh berbeda dengan mencari turunan fungsi biasa.
Untuk lebih jelasnya Perhatikan contoh-contoh soal dibawah ini, bagaimana mencari turunan fungsi implisit.
Contoh :
Tentukan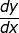 
dari setiap fungsi Implisit dibawah ini!
dari setiap fungsi Implisit dibawah ini!
[Penyelesaian]
Turunkanlah kedua ruas terhadap x,
[Penyelesaian]
Turunkanlah kedua ruas terhadap x,
[penyelesaian]
Turunkanlah kedua ruas terhadap x
[Penyelesaian]
Turunkanlah kedua ruas terhadap x
[Penyelesaian]
Turunkanlah kedua ruas terhadap x
Beberapa kasus dapat diselesaikan dengan 2 cara yaitu:
Cara I :
x3-3x2y+y2=0
3x2-6xy-3x2dydx+2ydydx=0
dydx(-3x2+2y)=-3x2+6xy
dydx=-3x2+6xy-3x2+2y
Cara II:
x3-3x2y+y2=0
3x2dx-6xy dx-3x2dy+2y dy=03x2-6xy-3x2dydx+2ydydx=0:dx
dydx(-3x2+2y)=-3x2+6xy
dydx=-3x2+6xy-3x2+2y
Tidak ada komentar:
Posting Komentar